Person Re-Identification by Manifold Ranking ICIP'13

Introduction

Existing person re-identification methods conventionally rely on labelled pairwise data to learn a task-specific distance metric for ranking. The value of unlabelled gallery instances is generally overlooked. In this study, we show that it is possible to propagate the query information along the unlabelled data manifold in an unsupervised way to obtain robust ranking results. In addition, we demonstrate that the performance of existing supervised metric learning methods can be significantly boosted once integrated into the proposed manifold ranking (MRank)-based framework. Extensive evaluation is conducted on three benchmark datasets.

Contribution Highlights

  • We investigate the importance of using unlabelled gallery data for rank diffusion, which has been largely neglected by previous re-identification studies.
  • We systematically formulate and validate existing MRank models for the re-identification task.
  • We show that existing supervised metric learning methods can benefit from the unsupervised MRank framework to gain improved performance.

Citation

  1. Person Re-Identification by Manifold Ranking
    C. C. Loy, C. Liu, and S. Gong
    in Proceedings of IEEE International Conference on Image Processing, pp. 3567-3571, 2013 (ICIP)
     PDF Poster

Images

A two-dimensional manifold embedding of gallery images:

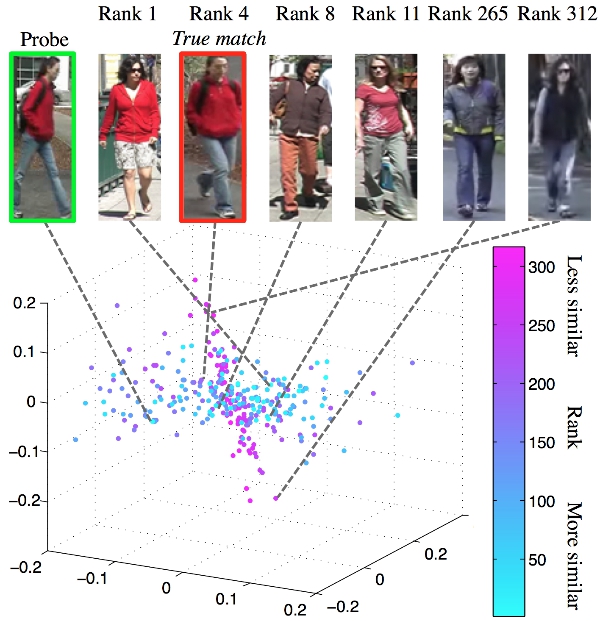
The two-dimensional manifold embedding exhibit two obvious clusters. Images visually similar to the probe mostly reside on the blue circular region, whilst dissimilar images can be found in the pink ellipsoid region. One can imagine that visual ranking would be more effective in this manifold space.

Manifold ranking results:

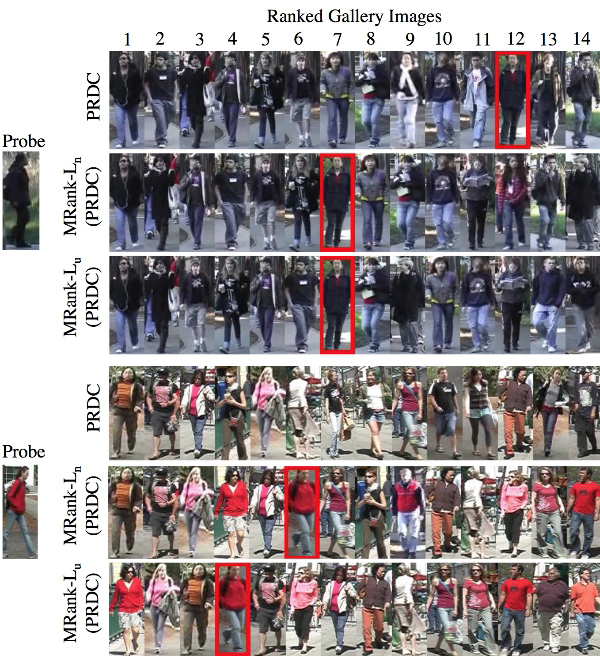
Example results by manifold ranking (MRank), compared against that obtained by PRDC without manifold ranking. The left-most image is the probe. The true match within the ordered gallery candidates is highlighted with red border.

\( \beta \) sensitivity test: CMC curves with \( \beta = 10^{-2} \)

\( \beta \) sensitivity test on the unnormalised Laplacian (\( L_u \)) and normalised Laplacian (\( L_n \)). PRDC was used to initialise MRank.

\( \beta \) sensitivity test: Area under the CMC (AUCMC) with \(\beta\) varied from \(10^{-5}\) to \(10\).

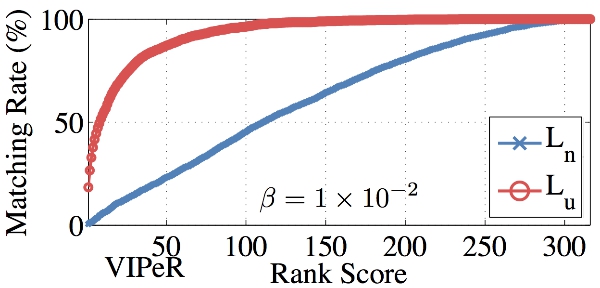
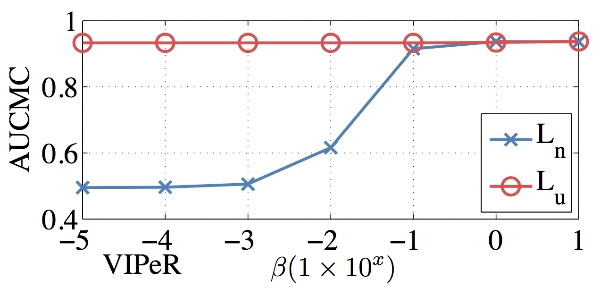
\( \beta \) sensitivity test on the unnormalised Laplacian (\( L_u \)) and normalised Laplacian (\( L_n \)). PRDC was used to initialise MRank.

Datasets and Codes

UnderGround Re-IDentification (GRID) Dataset

The QMUL underGround Re-IDentification (GRID) dataset contains 250 pedestrian image pairs. Each pair contains two images of the same individual seen from different camera views. In addition, there are 775 extra individual images that do not belong to any of the paired images. All images are captured from 8 disjoint camera views installed in a busy underground station. The dataset is challenging due to variations of pose, colours, lighting changes; as well as poor image quality caused by low spatial resolution.

Details ...
MATLAB code for manifold ranking

MATLAB implementation of normalised graph Laplacian presented in [1] and unnormalised iterated graph Laplacian presented in [2].

  1. D. Zhou, J. Weston, A. Gretton, O. Bousquet, and B. Scholkopf, "Ranking on data manifolds," in NIPS, 2004, vol. 16, pp. 169-176
  2. X. Zhou, M. Belkin, and N. Srebro, "An iterated graph Laplacian approach for ranking on manifolds," in SIGKDD, 2011, pp. 877-885.

Download Codes [51 KB]

Supplementary Materials

  • Averaged cumulative match characteristic (CMC) curve of 10 trials. Download

Related Projects